コリオリ力を理解する

回転座標系にいる人にとって、
ωの角速度で回転座標系で速度vで動いている物体は
動いている方向の直角方向に2mωvの力が
働いてるように見える。(mは質量)

この力をコリオリ力と呼ぶ。


このコリオリ力について参考書を見ると、
たいてい微分とかによって式展開をしているが、
計算式を見せられても計算はわかるが
コリオリ力に関して直感的にわからない。

ということで、遠心力を求めたときと同じように、
直感的にわかりやすいと思われる図をつけて理解していく。
(この後の説明は遠心力を理解するを読んだ前提で説明してある)



まず、外の静止系から見て点Oを中心として反時計周りに回転している板の上に
板の上から見ると止まっている物体があるとする。

その物体は板の外の静止系から見ると、rωの速度で動いてるように見える。
(板の回転の角速度をω、点Oと物体の距離をrとする)
t秒でのこの物体の板の回転による速度をV回(t)とする。(|V回(t)|=rω)

-------------------
次に、回転している板の上で物体がt秒の時v上(t)の速度で動いたと考える。
(v上(t)は、V回(t)と平行としておく。詳細は下図を参照)

板の外の静止系から見ると物体はV回(t)+v上(t)の速度で動いてるように見える。
（上図では、薄緑色で書かれている）

ここで、点Oからt秒の物体の位置の方向をx軸、V回(t)の方向をy軸とする
xy座標を考える。

板の上から見て物体はv上(t)の速度で動くため、
t秒ではxy座標で見て、(x,y)=(r,0)にあった物体が、
Δt秒後にはxy座標からΔθ回転したx'y'座標で見て、
(x',y')=(r, |v上(t)|Δt)に物体が存在するようになる。（下図参照）
(Δθ=ωΔtである)

Δt秒後の静止系から見た板の回転による部分の物体の速度はV回(t+Δt)、
Δt秒後の回転する板の上から見た物体の速度はv上(t+Δt)とすると、
Δt秒後の物体の静止系から見た速度は、V回(t+Δt)+v上(t+Δt)となる。

Δt秒の間の静止系から見た速度ベクトルの変化をΔtで割ったのが
加速度ベクトルとなるので、
(V回(t+Δt)+v上(t+Δt))-(V回(t)+v上(t))=a(t)Δt
(a(t)は物体の加速度ベクトル。
上の図の右下あたりに薄緑色でベクトルの絵が書かれている)

ゆえに、加速度を求めるには、(V回(t+Δt)+v上(t+Δt))-(V回(t)+v上(t))を計算する必要がある。

(V回(t+Δt)+v上(t+Δt))-(V回(t)+v上(t))=(V回(t+Δt)-V回(t))+(v上(t+Δt)-v上(t))となるので、
図を見ながら、(V回(t+Δt)-V回(t))と、(v上(t+Δt)-v上(t))を計算する。

板の上から見た物体の速度の大きさは変わるわけがないので、|v上(t)|=|v上(t+Δt)|
v上(t)とv上(t+Δt)の間の角度は、Δθとなるので(Δθ=ωΔtである)、
遠心力の時の計算と同じような計算をすると、Δt→0で
v上(t+Δt)-v上(t)=|v上(t)|ωΔt×(-e⊥)　-①
(e⊥はV回(t)と垂直で円の外側方向の単位ベクトル。
遠心力の時と同じ計算はこちら)

V回(t)とV回(t+Δt)の間の角度は、Δθ+Δφとなる。
(Δφは上の図に書いてあるが、Δt秒後の物体の位置(x',y')=(r,|v上(t)|Δt)をA、
x'y'座標で(x',y')=(r,0)となる位置をBとしたときの∠AOBをΔφとしている。
ちなみにtanΔφ=|v上(t)|Δt/rとなる。)
さらに、Δt→0の時、Δφ=|v上(t)|Δt/rと考えていい。

物体と点Oからの距離はΔt秒後にr(t+Δt)になる。
r(t+Δt)=r+O(Δφ²)=r+O(Δt²)となるので
(遠心力の理解の補足と同じように計算　（遠心力の補足の計算はこちらの下の方にある）)、
Δt→0でO(Δt²)の部分が加速度ベクトルを求める時は0になる。
なので、r(t+Δt)=rと考えても差支えがない。
(O(Δφ²)は、k2Δφ²+k3Δφ³+・・・で、k2、k3・・・は有限)

|V回(t+Δt)|=r(t+Δt)ω=rωとなり、|V回(t+Δt)|=|V回(t)|と考える。
これも、遠心力の時の計算と同じような計算をすると、Δt→0で
V回(t+Δt)-V回(t)=|V回(t)|(Δθ+Δφ)×(-e⊥)=rω²Δt×(-e⊥)+|v上(t)|ωΔt×(-e⊥) -②
（遠心力の時と同じ計算はこちら）

①と②より、
a(t)Δt=(V回(t+Δt)+v上(t+Δt))-(V回(t)+v上(t))
=(V回(t+Δt)-V回(t))+(v上(t+Δt)-v上(t))
=rω²Δt×(-e⊥)+2ω|v上(t)|Δt×(-e⊥)

ゆえに、加速度ベクトルa(t)=rω²×(-e⊥)+2ω|v上(t)|×(-e⊥)

見かけの力は加速度ベクトルと逆方向に働くので(慣性力を理解するに書いた)、
見かけの力は、ma(t)=mrω²×e⊥+2mω|v上(t)|×e⊥

mrω²×e⊥は遠心力の部分で、2mω|v上(t)|×e⊥はコリオリ力の部分である。
物体が板に対して進む速度の向きとは直角で右方向にコリオリ力が働くことになる。

コリオリ力の大きさは2mω|v上(t)|


-----------------------
さらに次に、
回転している板の上で物体がt秒の時v横(t)の速度で動いたと考える。
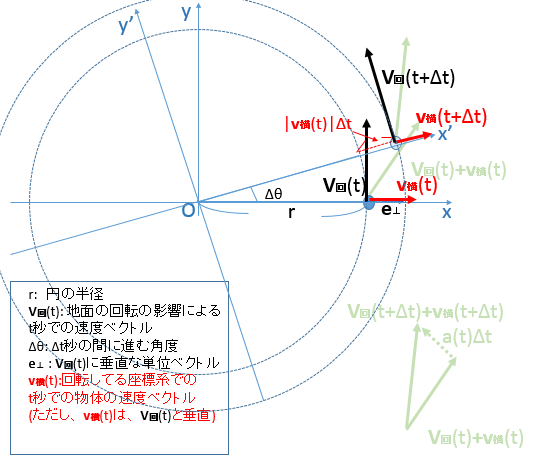
(v横(t)は、V回(t)と垂直としておく。詳細は下図を参照)

板の外の静止系から見ると物体はV回(t)+v横(t)の速度で動いてるように見える。
（上図では、薄緑色で書かれている）

ここで、点Oからt秒の物体の位置の方向をx軸、V回(t)の方向をy軸とする
xy座標を考える。

板の上から見て物体はv横(t)の速度で動くため、
t秒ではxy座標で見て、(x,y)=(r,0)にあった物体が、
Δt秒後にはxy座標からΔθ回転したx'y'座標で見て、
(x',y')=(r+|v横(t)|Δt,0)に物体が存在するようになる。（下図参照）
(Δθ=ωΔtである)

Δt秒後の静止系から見た板の回転による部分の物体の速度はV回(t+Δt)、
Δt秒後の回転する板の上から見た物体の速度はv横(t+Δt)とすると、
Δt秒後の物体の静止系から見た速度は、V回(t+Δt)+v横(t+Δt)となる。

Δt秒の間の静止系から見た速度ベクトルの変化をΔtで割ったのが
加速度ベクトルとなるので、
(V回(t+Δt)+v横(t+Δt))-(V回(t)+v横(t))=a(t)Δt
(a(t)は物体の加速度ベクトル。
上の図の右下あたりに薄緑色でベクトルの絵が書かれている)

ゆえに、加速度を求めるには、(V回(t+Δt)+v横(t+Δt))-(V回(t)+v横(t))を計算する必要がある。

(V回(t+Δt)+v横(t+Δt))-(V回(t)+v横(t))=(V回(t+Δt)-V回(t))+(v横(t+Δt)-v横(t))となるので、
図を見ながら、(V回(t+Δt)-V回(t))と、(v横(t+Δt)-v横(t))を計算する。

板の上から見た物体の速度の大きさは変わるわけがないので、|v横(t)|=|v横(t+Δt)|
v横(t)とv横(t+Δt)の間の角度は、Δθとなるので(Δθ=ωΔtである)、
遠心力の時の計算と同じような計算をすると、Δt→0で
v横(t+Δt)-v横(t)=|v横(t)|ωΔt×e//　-③
(e//はV回(t)と垂直で円の外側方向の単位ベクトル。遠心力の時と同じ計算はこちら)

V回(t)とV回(t+Δt)の間の角度は、Δθとなる。

物体と点Oからの距離はΔt秒後にr+|v横(t)|Δtになる。
|V回(t+Δt)|=(r+|v横(t)|Δt)ωとなる。
一方、|V回(t)|=rω
なので、
V回(t+Δt)=|V回(t+Δt)|×(V回(t+Δt)/|V回(t+Δt)|)
=(r+|v横(t)|Δt)ω×(V回(t+Δt)/|V回(t+Δt)|)
=|V回(t)|×(V回(t+Δt)/|V回(t+Δt)|)+|v横(t)|Δtω×(V回(t+Δt)/|V回(t+Δt)|)　-④

||V回(t)|×(V回(t+Δt)/|V回(t+Δt)|)|=|V回(t)|で、
|V回(t)|×(V回(t+Δt)/|V回(t+Δt)|)とV回(t)の間の角度はΔθなので、
遠心力の時の計算と同じような計算をすると、Δt→0で
|V回(t)|×(V回(t+Δt)/|V回(t+Δt)|)-V回(t)=|V回(t)|Δθ×(-e⊥)=rω²Δt×(-e⊥)　-⑤
（遠心力の時と同じ計算はこちら）





④と⑤より、
V回(t+Δt)-V回(t)=|v横(t)|Δtω×(V回(t+Δt)/|V回(t+Δt)|)+rω²Δt×(-e⊥) -⑥

③と⑥より、
a(t)Δt=(V回(t+Δt)+v横(t+Δt))-(V回(t)+v横(t))
=(V回(t+Δt)-V回(t))+(v横(t+Δt)-v横(t))
=rω²Δt×(-e⊥)+ω|v横(t)|Δt×(e//)+|v横(t)|Δtω×(V回(t+Δt)/|V回(t+Δt)|)

V回(t+Δt)/|V回(t+Δt)|は、単位ベクトルである。
V回(t)と垂直で円の外側方向の単位ベクトルe//とV回(t+Δt)/|V回(t+Δt)|の間の角度は
Δθである。e//とV回(t+Δt)/|V回(t+Δt)|は微小しか違わないので、
e//=V回(t+Δt)/|V回(t+Δt)|としてしまっていい。

ゆえに、先ほどの計算は
a(t)Δt=(V回(t+Δt)+v横(t+Δt))-(V回(t)+v横(t))
=(V回(t+Δt)-V回(t))+(v横(t+Δt)-v横(t))
=rω²Δt×(-e⊥)+2ω|v横(t)|Δt×(e//)

ゆえに、加速度ベクトルa(t)=rω²×(-e⊥)+2ω|v横(t)|×(e//)

見かけの力は加速度ベクトルと逆方向に働くので(慣性力を理解するに書いた)、
見かけの力は、ma(t)=mrω²×e⊥+2mω|v横(t)|×(-e//)

mrω²×e⊥は遠心力の部分で、2mω|v横(t)|×(-e//)はコリオリ力の部分である。
物体が板に対して進む速度の向きとは直角で右方向にコリオリ力が働くことになる。

コリオリ力の大きさは2mω|v横(t)|


物体がV回(t)と同じ方向に動いても、V回(t)と垂直の方向に動いても
コリオリ力は2mω×速度vとなる。

コリオリ係数は2ωである。


-------
じゃあ、物体がV回(t)とは斜めの方向に動いたときコリオリ力はどうなるか？

回転している板の上で物体がt秒の時、v横(t)+v上(t)の速度で動いたと考える。
(V回(t+Δt)+v横(t+Δt)+v上(t+Δt))-(V回(t)+v横(t)+v上(t))を今までと同じように求めれば、
コリオリ力が求まるであろう。(下図参照)

結果は、v横(t)+v上(t)のベクトルにたいして直角の方向で右方向に
2mω|v横(t)+v上(t)|のコリオリ力が働く。
(めんどくさいので計算は省く)


実は、参考書のコリオリ力を求める計算はこれをやっているだけである。

正直言って僕の図もコリオリ力が直感的にわかりにくいかもしれない。

コリオリ力が直感的にわかりにくい理由は
v上(t)の時は、V回(t+Δt)とV回(t)の間の角度がΔθ+Δφで、|V回(t+Δt)|=|V回(t)|であるが、
v横(t)の時は、V回(t+Δt)とV回(t)の間の角度がΔθで、|V回(t+Δt)|=|V回(t)|+rωΔtと、
v上(t)の時とv横(t)の時とでは、V回(t+Δt)の性質が変わるためである。

ただ、違うような計算をしているのに、最終的にv上(t)の時もv横(t)の時も
コリオリ力は2mωvとなるのはすごいと思う。




-----------------
スポンサードリンク

-----------------



Tweet